Thompson Sampling in Bernoulli Bandits

In this post, I will implement Thompson Sampling in a Bernouli bandit problem in Python and compare it with the performance of the greedy algorithm. This page is simply implementing the algorithms elegantly explained in this paper.

import numpy as np
import math 
import matplotlib.pyplot as plt

This is the implementation of the greedy algorithm in the paper

def greedy_update_posterior_params(T, rewards):
    beta = [1 for _ in rewards]
    alpha = [1 for _ in rewards]
    bins = np.linspace(0, 1, 100)
    for t in range(1,T+1):
        theta = []
        for k in range(len(rewards)):
            theta.append(alpha[k]/(alpha[k]+beta[k]))
        max_idx = max(range(len(rewards)), key=lambda i:theta[i])
        r = rewards[max_idx]
        beta[max_idx] += 1-r
        alpha[max_idx] += r
        if t % 100 == 0:
            plt.figure(figsize=(14,4))
            for j in range(len(rewards)):
                armj = [np.random.beta(alpha[j], beta[j]) for _ in range(1000)]
                plt.hist(armj, bins, alpha=0.5, label='arm {}'.format(j))
            plt.legend(loc='upper right')
            plt.show()
         
    return alpha, beta

Here is also the implementation of the Thompson Sampling algorithm for the Bernoulli bandit with Beta prior distribtuion.

def thompson_sampling_update_posterior_params(T, rewards):
    beta = [1 for _ in rewards]
    alpha = [1 for _ in rewards]
    bins = np.linspace(0, 1, 100)
    for t in range(1,T+1):
        theta = np.random.beta(alpha, beta).tolist()
        max_idx = max(range(len(rewards)), key=lambda i:theta[i])
        r = rewards[max_idx]
        beta[max_idx] += 1-r
        alpha[max_idx] += r
        if t % 100 == 0:
            plt.figure(figsize=(14,4))
            for j in range(len(rewards)):
                armj = [np.random.beta(alpha[j], beta[j]) for _ in range(1000)]
                plt.hist(armj, bins, alpha=0.5, label='arm {}'.format(j))
            plt.legend(loc='upper right')
            plt.show()
            
    return alpha, beta

Here is the result of running these algorithms

alpha, beta = greedy_update_posterior_params(500,  [0.1,0.8,0.6,0.3])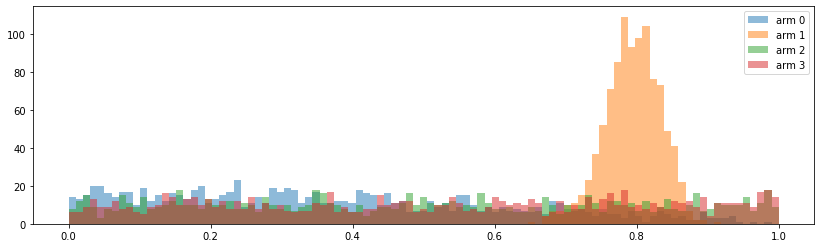

Greedy Algorithms

alpha, beta = thompson_sampling_update_posterior_params(500,  [0.1,0.8,0.6,0.3])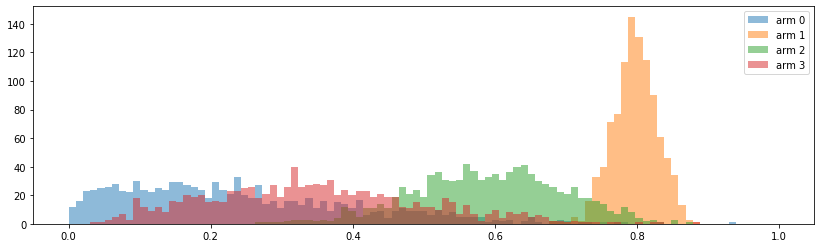

Thompson Sampling A summary of this code is available in this notebook.